题目内容
（请给出正确答案）
设有n阶多项式f(x)=anxn+an-1xn-1+...+a0证明:若将它改写为
f(x)=bn(x-a)n+bn-1(x-a)n-1+...+b0,
则
k=1,2...,n.f(0)(a)=f(a).
如果结果不匹配，请 联系老师 获取答案
更多“设有n阶多项式f(x)=anxn+an-1xn-1+...+…”相关的问题
设A是复数域C上一个n阶矩阵，λ1，λ2，···，λn是A的全部特征根(重根按重数计算)。
(i)如果f(x)是C上任意一个次数大于零的多项式，那么f(λ1)，f(λ2)，···，f(λn)是f(A)的全部特征根;
(ii)如果A可逆，那么λi≠0，i=1，2，...，n，并且
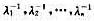是A-1的全部特征根。
令Fn[x]是某一数域F上全体次数≤n的多项式连同零多项式所组成的向量空间。令：
。求出σ的最小多项式。
证明:函数f(x)是n次多项式,a是方程f(x)=0的k(k≤m)重根
f
(a)=f´(a)==f(k-1)(a)=0,而f(k)(a)≠0.
设a1，a2，...，an是n个不同的数，而F(x)=(x-a1)(x-a2)...(x-an)，b1，b2，...，bn是任意n个数，显然
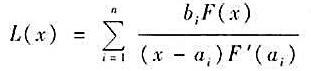适合条件L(ai)=bi，i=1，2，...，n。这称为拉格朗日(Lagrange)插值公式。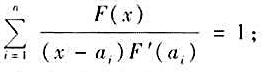
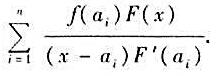
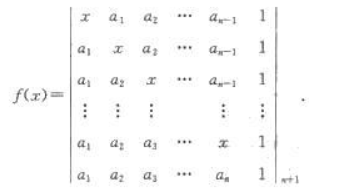
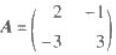利用上面的公式求：
1)一个次数＜4的多项式f(x)，它适合条件：f(2)=3，f(3)=-1，f(4)=0，f(5)=2。
2)一个二次多项式f(x)，它在x=0，2/π，π处与函数sinx有相同的值。
3)一个次数尽可能低的多项式f(x)，使f(0)=1，f(1)=2，f(2)=5，f(3)=10。
设a1，a2，...，an是n个不同的数，而F(x)=(x-a1)(x-a2)...(x-an)。证明：
1)
2)任意多项式f(x)用F(x)除所得的余式为
如果f(x)=3-5x+x2，
，求f(A)。
