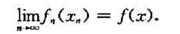题目内容
（请给出正确答案）
[主观题]
证明:若函数项级数在[a,b]一致收敛于和函数S(x),且函数un(x)在[a,b]可积,则和函数S(x)在[
证明:若函数项级数在[a,b]一致收敛于和函数S（x),且函数un（x)在[a,b]可积,则和函数S（x)在[
证明:若函数项级数![证明:若函数项级数在[a,b]一致收敛于和函数S（x),且函数un（x)在[a,b]可积,则和函数S](https://img2.soutiyun.com/ask/2020-11-13/974118907131862.jpg)
在[a,b]一致收敛于和函数S(x),且![证明:若函数项级数在[a,b]一致收敛于和函数S（x),且函数un（x)在[a,b]可积,则和函数S](https://img2.soutiyun.com/ask/2020-11-13/974118929095118.png)
函数un(x)在[a,b]可积,则和函数S(x)在[a,b]也可积.
查看答案
如果结果不匹配，请 联系老师 获取答案
更多“证明:若函数项级数在[a,b]一致收敛于和函数S(x),且函…”相关的问题
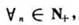函数φn(x)在[a,b]单调,且级数
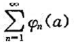与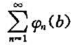
都绝对收敛,则函数项级数
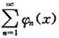在[a,b]一致收敛.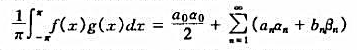
在区间[-a,a](a＞0)一致收敛,在R非一致收敛.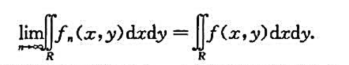
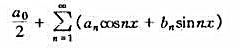
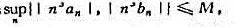
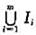也一致收敛.
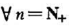,xn∈[a,b],且xn→x(n→∞),则
